Chapter 9 Before we start…
Prior to beginning to prove some conjectures, there are several questions which students always have, or difficulties that seem to arise. This chapter will address some of them.
9.1 How do I write a good proof?
Here are some things to remember when writing proofs:
- Label lines of work that you need to refer back to with reference numbers. In this course, you should also label the conjecture with the reference number from the textbook. End the proof with the \(\square\) symbol to show you’re done.
Good mathematical proofs written by one person should be understandable by another. All terms should be clearly defined, and any variables used too.
Proofs should be watertight, meaning that it shouldn’t contain any holes - no one should be able to criticise you for not considering something. For example, if the conjecture concerns all whole numbers, your proof would not be valid if it only covers positive numbers. If the statement concerns all polygons, your proof would not be valid if it only covers triangles and squares.
Proofs should always be as short and efficient as possible, whilst still being complete.
9.2 How do I check my proof is correct?
Mathematicians can’t check their own proofs, mainly because they wrote it. Have you ever tried to spot a mistake you’ve made in your own work? It can be really difficult to do!
For a proof to be declared valid, it should be shared with your peers to check it. Germain did this, Mirzakhani did this, Euclid did this. In this course, you’ll share your answers with me and with each other.
Once your peers have approved it, you then can publish your proof as a piece of mathematics. It’s at this point that you enter the history books and your mathematical proof remains valid for ever!
Note: As you move through the rest of this course, you will start to get a sense of when you have finished a proof. Knowing when a proof is finished, and when it is not finished, is a valuable skill you will develop.
9.3 Key things to bear in mind when proving
You can’t prove a conjecture using examples unless you can be sure that the examples cover all possible instances of the conjecture. Even if the conjecture holds for the first few examples you try, this is no guarantee that the conjecture is always true. Let’s look at a couple of examples.
Conjecture 9.1 : If \(a\) is a prime number then so is \(2^a - 1\).
Whilst this conjecture holds for \(a=2\), \(a=3\), \(a=5\), \(a=7\) (the first four primes), the conjecture breaks at \(a = 11\), because \(a^{11} - 1 = 2047\) which isn’t prime (it’s divisible by both \(23\) and \(89\)).
Conjecture 9.2 : \(a^2 - a + 11\) is prime, for \(a \in \mathbb Z^+\)
holds for all values of \(a\) from \(1\) to \(10\) but breaks at \(a= 11\).
You must define any variables you introduce. For example, if you are told that \(a\) is odd and you decide to express it as \(a = 2k + 1\), you should tell your reader what \(k\) is (in this case, \(k\) is an integer).
Don’t assume the thing to be proved is true. If you are trying to prove something is true, you can’t assume it is true at the beginning of the proof. The reason for this is because assuming it true at the beginning might encourage you to use it as an established fact during your proof.35
You mustn’t claim something is true without having justified it. This might simply involve showing it to be true in the proof, or referring to a previously proved conjecture.
Note: The first of these means you haven’t actually started a proof. The second is not too much of a problem and is easily rectified. The last two would mean you have started a proof but that it contains fundamental problems.
9.4 Some useful arrows
The arrows \(\Rightarrow\), \(\Leftarrow\), \(\Leftrightarrow\) describe relationships that can be represented with Venn diagrams.
For sets \(A\) and \(B\):
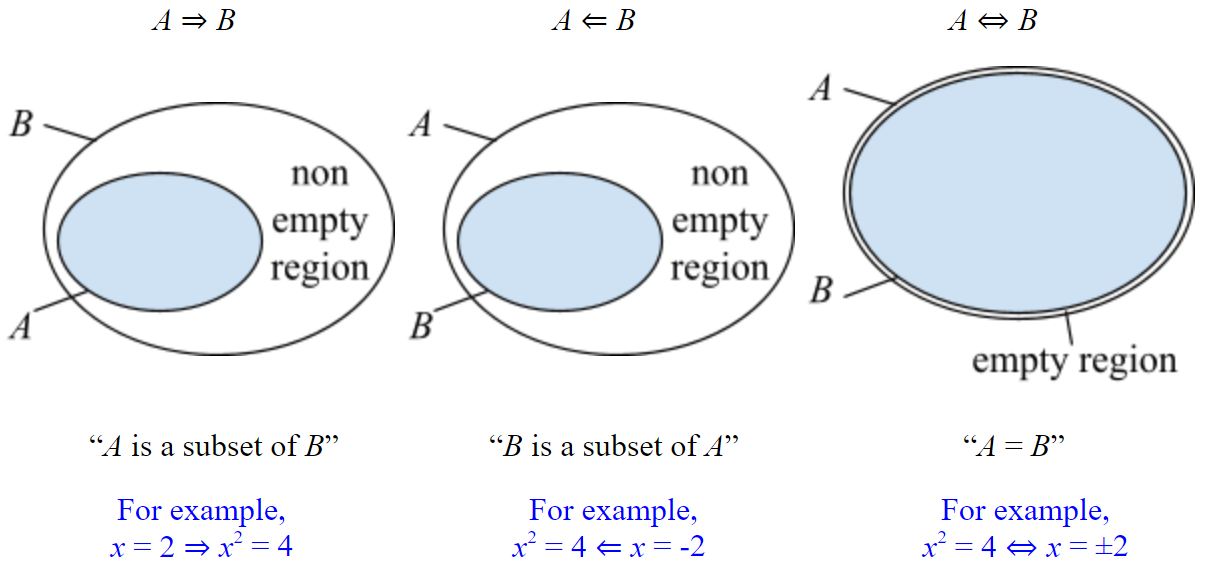
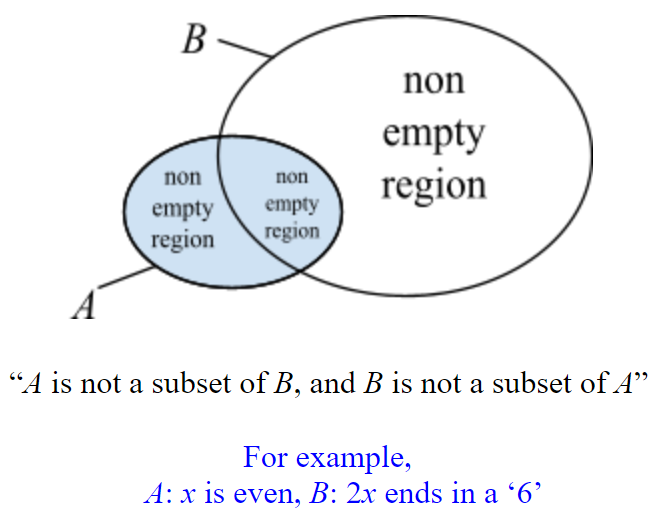
If \(A\) is not a subset of \(B\), or \(B\) is not a subset of \(A\), then we cannot use these arrows:
- The animal is human
The animal has a brain - The animal can fly
The animal is a bird - The animal has feathers
The animal is a bird - The animal knows which year Coca-Cola was founded
The animal is human - The animal lays eggs
The animal is a bird - The animal’s species has been to the Moon
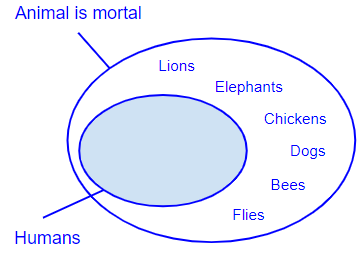
The animal is human - The animal is mortal
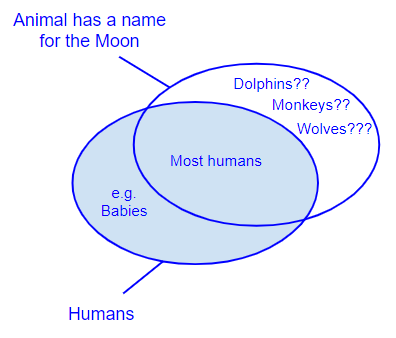
The animal is human - The animal has a name for the Moon
The animal is human
Solutions, including some Venn diagrams:
- The animal is human ⇒ The animal has a brain

- The animal can fly N/A The animal is a bird

- The animal has feathers ⇔ The animal is a bird
- The animal knows which year Coca-Cola was founded ⇒ The animal is human
- The animal lays eggs ⇐ The animal is a bird
- The animal’s species has been to the Moon ⇔ The animal is human
- The animal is mortal ⇐ The animal is human
- The animal has a name for the Moon N/A The animal is human
- The number is 3
The number is odd - The number is odd
The number is positive - The number is divisible by 2
The number is even - The number is not divisible by 2
The number is odd - The number is a multiple of 5
The number ends in a ‘5’ - The number is irrational
The number is not an integer - The number squared is zero
The number is zero - The number squared is one
The number is one
Solutions:
- The number is 3 ⇒ The number is odd
- The number is odd N/A The number is positive
- The number is divisible by 2 ⇔ The number is even
- The number is not divisible by 2 ⇐ The number is odd

- The number is a multiple of 5 ⇐ The number ends in a ‘5’
- The number is irrational ⇔ The number is not an integer
- The number squared is zero ⇔ The number is zero
- The number squared is one ⇐ The number is one
Exercise 9.3 Add either “⇒,” “⇐” or “⇔” to the following, to make them correct. If neither arrow is correct, write N/A. Draw a Venn diagram to summarise each answer. Solutions are below.
Note: Polygons are straight-edged 2D closed shapes. Polygons come in two flavours, convex and concave. See: https://mathworld.wolfram.com/ConvexPolygon.html.- The polygon has three sides
The polygon is a triangle - The polygon has three sides
The polygon is convex - The polygon has four sides
The polygon is convex - The polygon is concave
The polygon has at least four sides - The polygon is regular
The polygon has an even number of sides - The polygon has exactly four right-angles
The polygon is a square - The polygon has exactly four lines of symmetry
The polygon is a square - The polygon has no lines of symmetry
The polygon is not regular
Solutions:
- The polygon has three sides ⇔ The polygon is a triangle
- The polygon has three sides ⇒ The polygon is convex
- The polygon has four sides N/A The polygon is convex
- The polygon is concave ⇒ The polygon has at least four sides
- The polygon is regular N/A The polygon has an even number of sides
- The polygon has exactly four right-angles ⇐ The polygon is a square
- The polygon has exactly four lines of symmetry ⇔ The polygon is a square
- The polygon has no lines of symmetry ⇒ The polygon is not regular
- The UN member state has a non-rectangular flag
The UN member state is Nepal - The UN member state has only red and yellow on its flag
The UN member state is c. The Kyrgyz Republic - The UN member state joined the UN in the 2000’s (i.e. between 1st Jan 2000 and 31st Dec 2009)
The UN member state is Serbia - The UN member state has more than one official language
The UN member state is in Africa - The country is a member of the UN
The country is a member of the EU - The UN member state has a sun depicted on its flag
The UN member state is predominantly in situated in the Northern hemisphere - The UN member state is an island nation
The UN member state has a population smaller than 5 million - The UN member state has disputed borders with at least one other UN member state
The UN member state joined the UN in the 1940’s
Solutions:
- The UN member state has a non-rectangular flag ⇔ The UN member state is Nepal
- The UN member state has only red and yellow on its flag ⇐ The UN member state is The Kyrgyz Republic
- The UN member state joined the UN in the 2000’s (i.e. between 1st Jan 2000 and 31st Dec 2009) ⇐ The UN member state is Serbia
- The UN member state has more than one official language N/A The UN member state is in Africa
- The country is a member of the UN ⇐ The country is a member of the EU
- The UN member state has a sun depicted on its flag N/A The UN member state is predominantly in situated in the Northern hemisphere
- The UN member state is an island nation N/A The UN member state has a population smaller than 5 million
- The UN member state has disputed borders with at least one other UN member state N/A The UN member state joined the UN in the 1940’s
9.5 Example
Let’s look at an example of a good proof and a bad proof. Both are trying to prove the following conjecture:
Conjecture 9.3 : If \(a\) is odd, the \(3a\) is odd.
9.5.1 A good proof
First, the good proof.
Proof. Our starting point, \(P\), is that \(a\) is odd. As \(a\) is odd, we can express it as \[\begin{align} a &= 2k + 1 \tag{9.1} \end{align}\] where \(k\) is an integer. Then \[\begin{align} 3a &= 3(2k + 1) \tag{9.2} \\ &= 6k + 3 \tag{9.3} \\ &= 6k + 2 + 1 \tag{9.4} \\ &= 2(3k + 1) + 1 \tag{9.5} \end{align}\] which is odd.
Here are a couple of things to notice:
This conjecture was not difficult to prove, so the proof shouldn’t be overly complicated. The presentation above demonstrates how to write a clear, comprehensive, cohesive and rigorous (watertight) argument.
We label the conjecture with its reference number from the textbook, in this case “Conjecture 9.3,” so that if we need to we can refer back to it and its proof/disproof later. As we’ll see in a later chapter, we often use work we’ve done previously, and having a quick way to refer back to previous conjectures and their proofs/disproof can speed this up for us!
Every line in the proof above is labelled with a reference number: (9.1), (9.2), (9.3), (9.4), (9.5). In your proofs, you probably won’t need or want to label every line of work, but you should label important lines, ones which you use later in the proof (or even later in proofs of other conjectures!)
Notice that we used the \(\square\) symbol to indicate that we consider the proof is finished.
9.5.2 A bad proof
Now for the bad proof.
\[\begin{align} a = 2k + 1 &= 3(2k + 1) \\ &= 2(3k + 1) + 1 \end{align}\]
Whilst the same reasoning underpins this proof as the proof above, it is far from easy to understand for the reader. Also, not writing out each step means the author of the proof runs the risk of making mistakes, which are then harder to spot. Finally, there are some plain mathematical mistakes (\(2k + 1 \neq 3(2k + 1)\)), even though we know what the author meant!
Exercise 9.5 Look back at the “bad proof” above. Based on everything you’ve read in this chapter, how many things can you find to criticise about this proof?
A lawyer in court trying to prove a defendant guilty is not allowed to say, “Because we know the defendant is guilty, we know he can’t have been where he says he was on the night of the crime. Because we know he is guilty, we know he was at the scene of the crime that night.” No one in the jury is going to be convinced by this argument! The lawyer must find explicit evidence that the defendant was at the scene of the crime that night.↩︎