Chapter 8 Getting started with a new conjecture

Let’s take a moment to review what we’ve learnt over the past couple of chapters. In Chapter 5 we saw that axioms are statements which can’t be proved, because they are so fundamental. Axioms (and the even more fundamental definitions) are statements which allow us to talk about and do mathematics.

In Chapter 6 we learnt that any mathematical statement29 that we’re interested in proving or disproving can be reclassified a “conjecture.” We can then attempt to prove it or disprove it. In Chapter 7 we saw that the most common way of disproving a conjecture is to hunt for a counterexample.

In this chapter, we’ll formalise the steps you should follow upon meeting (or creating) a new conjecture, of whose truth value you don’t yet know. The steps are:

  1. Look for a counterexample.

  2. Attempt a proof:

  • Rewrite the statement in the form “If…then…”
  • If needed, draw the conjecture’s map.
  • Select the method(s) of proof.

8.1 Step 1: Start by looking for a counterexample

When beginning with a new conjecture, you (probably) don’t know whether it’s true or false. Therefore, your first step should always be to look for a counterexample. We saw in the last chapter that to disprove a false statement, we just need to find a single counterexample to disprove it.

If you find one, then you have disproved the conjecture, and don’t need to worry about trying to prove it (as you know it’s false!). If you don’t find one, it doesn’t mean there isn’t one, but at least you tried!

Looking for a counterexample is a good place to begin with a new conjecture because it helps you to understand what the conjecture is saying.

If you fail to find a counterexample, maybe the conjecture is true. Or maybe you just weren’t able to find a counterexample, even though one (or more) exists.30 Because we don’t know which, we move onto Step 2…

8.2 Step 2: Try to build a proof

We don’t know if the conjecture is true or false, but our attempts to disprove it by finding a counterexample failed. Our next step is to attempt to build a proof.

If the conjecture is true, we should be able to construct a proof to show this. If it is actually false, then as we build our proof we will find it breaks somehow. This would be called a disproof. Whilst finding a disproof is sufficient in showing the conjecture to be false, the disproof might make it easier to find a counterexample to the conjecture.

There are many different methods of proof we could build, and our choice will depend on the type of conjecture. We might have to try out several of the methods before we find the one that works. Also, different people might use different methods for the same conjecture. That’s fine. As long as they both come to the same conclusion about the conjecture’s truth value, the method used isn’t important.

8.2.1 If…then…

No matter what method you decide to start with, make sure the conjecture is in the form If … then …. If the conjecture is not in this form, rewrite it so that it is.

Why is the If … then …. form so important? The ‘if’ part signals the conjecture’s starting point, and the ‘then’ part signals the conjecture’s destination. It means we know where to begin our proof, and where we’re headed whilst we’re building the proof.

Example 8.1 Multiples of even numbers are even.

Rewritten in the If … then … form, this conjecture becomes “If \(a\) is an even number, then \(ka\) is even, where \(k \in \mathbb{Z}\).”

We use the letter \(P\) to indicate the starting point of a conjecture, and the letter \(Q\) to indicate the destination. So for the above conjecture:

Here are some more examples, taken from Exercise 6.1.1. The original conjecture is on the left, and the If … then … form on the right:

\(P\): \(a\) is an even number

\(Q\): \(ka\) is even, where \(k \in \mathbb{Z}\)

Original conjecture If … then …
All prime numbers are odd If \(p\) is prime, then \(p\) is odd
\((a + b)^2 = a^2 + b^2\) for any numbers \(a\) and \(b\) If \(a\) and \(b \in \mathbb{R}\), then \((a + b)^2 = a^2 + b^2\)
All sheep in South Africa are white If a sheep lives in South Africa, then it is white
The national flags of all UN members are rectangular If a country is a UN member, then its flag is rectangular
All numbers are either positive or negative If \(a \in \mathbb{R}\), then \(a\) is either positive or negative
\(a^2 > a\), where \(a\) is a whole number If \(a \in \mathbb{Z}\), then \(a^2 > a\)

8.2.2 Draw the map

Once the conjecture is in the form If … then …, you should attempt to draw the conjecture’s map.

It’s not always possible to draw a conjecture’s map, but if you’re able to it can really help you choose the most appropriate method of proof for that conjecture.

Here’s the format of a conjecture map:

Notice we start on the left side of the picture and finish on the right.

Next, we add \(P\) and \(Q\). We’ll use the conjecture from above, “If \(a\) is an even number, then \(ka\) is even, where \(k \in \mathbb{Z}\).”

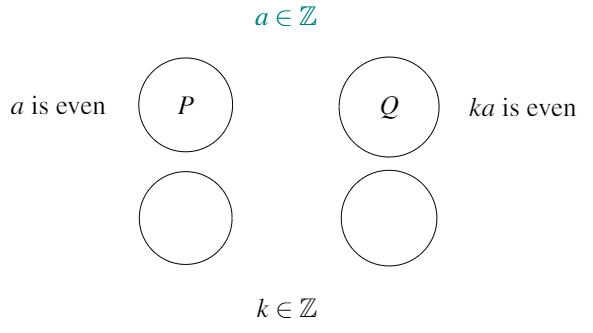
You can see that \(P\) has been added to the left side of the map and \(Q\) to the right side. Above the map we write what type of number we’re considering, in this case integers. Below the map, we write details of any variables (e.g. \(k\)) that the conjecture uses.

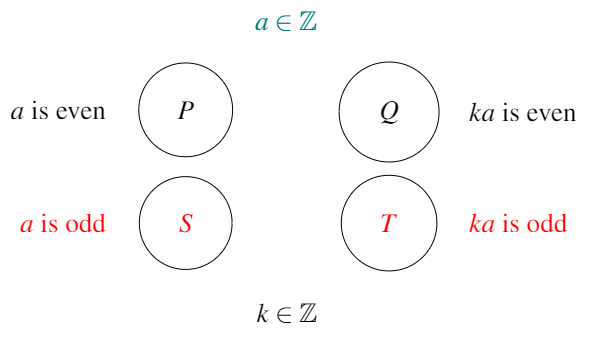
Next we add the opposite of \(P\) and the opposite of \(Q\) to the map.

What does the opposite mean? Well, in the example above, the numbers we’re considering are the integers. We put the even ones in \(P\), and all those which are not even (so odd) in \(S\) (see below).

Similarly, if you multiply an integer \(a\) (even or odd) by another integer (\(k\)), the result will be another integer. The even \(ka\) we’re storing in \(Q\), and the odd \(ka\) will go into \(T\).

Finally, we add arrows to the map to represent what the conjecture is saying. Arrows can only go from the left side of the map to the right side.

Therefore, the conjecture map of the statement “multiples of even numbers are even” is:

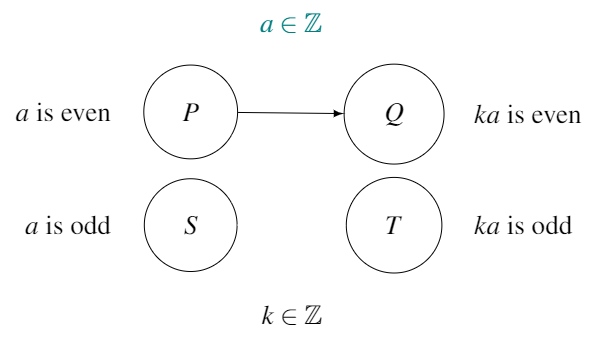
This can all seem really confusing, but trying to draw a couple of conjecture maps yourself will really help.

Conjecture maps rely on the idea of partitions. Let’s discuss what a partition of a set means.

8.2.3 Sets and subsets

First of all, what is a set? A set is simply a collection of items, called elements. For example, an AUCA course might be a set, and the elements would be students enrolled on the course. The set might be an alphabet, like the Kyrgyz alphabet, and the elements would be the 36 letters in this alphabet. Or the set might be the nonnegative integers, and the elements are the numbers \(0,1,2,3,4,...\).

Sets are denoted with a capital letter, and the elements in a set are placed within curly brackets. For example, \(A = \{\)Aibek, Aijamal, Aisuluu, Bektur, Maxim, Nurbek, Tammy\(\}\) might be the students enrolled on a course, or the first one-hundred positive integers would be written \(B = \{1, 2, 3, ..., 100\}\), and the set of all integers would be \(\mathbb{Z} = \{...,-3,-2,-1,-0,1,2,3,...\}\).

A set \(A\) is a subset of another set \(B\) if all of the elements of \(A\) are also in \(B\). We write this as \(A \subseteq B\). For example, if \(A\) is the set of students enrolled on a particular course at and \(B\) were the set of all AUCA students, then clearly \(A \subseteq B\). If it is known that \(A\) contains few elements than \(B\) (i.e. all elements of \(A\) are in \(B\) but there are some elements in \(B\) that are not in \(A\)) we can write \(A \subset B\). Here are another couple of examples: Kyrgyz vowels \(\subset\) Kyrgyz alphabet. Even integers \(\subset\) Integers.

8.2.4 Partitions

A partition of a set means breaking a set up into subsets where

  • no element is in more than one subset (i.e. subsets contain different elements to one another)
  • each element is in at least one subset (i.e. no element in the original set is forgotten)

An example would be during orientation for freshmen at AUCA: every student gets placed into a team, and no teams share any students.

For conjecture maps, you are required to partition sets into two subsets. An example would be classifying the integers as even or odd, classifying the integers as negative and nonnegative, classifying polygons into convex and concave, or classifying real numbers are rational31 or irrational.

Here are a few sample answers. Remember that when partitioning, the two subsets must be disjoint and together they must contain the entire (original) set.

  • Seniors and non-seniors;
  • Social science majors and non social science majors;
  • Students born in the Kyrgyz Republic and students born outside the Kyrgyz Republic;
  • Students who wear glasses and students who don’t wear glasses;
  • Students who’ve been to Turkey and students who’ve never been to Turkey;
  • ICP majors and non-ICP majors;
  • Students whose primary phone is a Samsung Galaxy and those whose primary phone is not a Samsung Galaxy (or they don’t have a phone);
  • Students who know how to say hello in Japanese and students who don’t know how to say hello in Japanese.

Bring your answers to our next class.

Solution:

  1. This is a valid partition: We can categorise everyone who lives in Bishkek as either having taken a trolleybus or having not a trolleybus.33

  2. This is not a valid partition: we have forgotten one-digit positive integers, like 4 or 7.

  3. This is not a valid partition, as there are some animals which are called semi-feral. These are animals that live mostly in the wild, but which have sporadic contact with humans, for example for feeding or medical attention. Also included in this group are animals which were born in a domesticated environment but which then escaped or were released into the wild, such as pet animals, laboratory animals, and some fish.

  4. This is a valid partition. All colours can be categorised as being primary (red, green or blue) or non-primary (for example, secondary colours such as yellow, tertiary colours such as azure, quaternary colours, and quinary colours).

  5. This is a valid partition, as positive numbers either are integers (with only zeros to the right of the decimal point) or non-integers (not only zeros to the right of the decimal point.

  6. This is not a valid partition, as there are some students who don’t smoke every day, but have smoked.

Solution:

  1. I would guess that the number of people in Bishkek who have never taken a trolleybus in their lives is much smaller than the number of people who have taken a trolleybus.

  2. There are only three primary colours and many more non-primary colours, so the subset containing the non-primary colours contains more elements.

  3. Even though there are an infinite number of positive integers and an infinite number of positive non-integers, the size of the infinity of the positive non-integers is larger! Watch the video mentioned in question 5 to learn more.

Solution:

  1. Answers will vary. For example, “positive integers with two digits” and “positive integers with more or less than two digits,” or “positive integers greater than 99” and “positive integers from 1 to 99.”

  2. Again, answers will vary. We could make this partition valid by including semi-feral animals in either subset, e.g. “completely wild” and “semi-feral and domesticated,” or “domesticated” and “not domesticated.

  3. For example, “has never smoked” and “has smoked.” Or “smokes every day” and “does not smoke every day.”

8.2.5 Choose your method

Once you have written the conjecture in the form “If … then …” and have attempted (hopefully successfully) in drawing its map, you are ready to begin to try building a proof.

We have lots of choices of methods of proof available. In this course, we’ll look at:

  • proof by exhaustion,
  • direct proof,
  • proof by cases,
  • proof via the contrapositive,
  • proof by contradiction, and
  • proof by induction.

Each of chapters 11 - 16 will cover one of these methods, and give you some examples to practice on.

At the end of each chapter there will be some more conjectures to work on. These conjectures might be true or might be false. To prove the true ones, you will be expected not just to rely on the method introduced in that chapter, but all previous methods too. This is because the challenge (and fun) of proving conjectures comes from not knowing where to start and feeling your own way to a proof. It’s a very satisfying experience!34

The next chapter, chapter 9, looks at what makes a good proof.

  1. Which is not an axiom or a definition.↩︎

  2. This could be for a number of reasons, such as the the counterexample(s) are really really big, or maybe because you forgot to check all types of examples. Also, maybe you were just unlucky.↩︎

  3. Check back to our textbook Chapter 5 if you’ve forgotten what rational numbers are.↩︎

  4. Two dimensional.↩︎

  5. We will say that those people who have sat in a stationary trolleybus but never a moving one as “not having taken a trolleybus.” We’ll say that people who have only ever been in trolleybuses that stopped working en-route to their destination as “having taken a trolleybus.”↩︎

  6. Also, when presented with a set of conjectures and told to “Prove using a direct proof…” or “Prove by induction…,” like a robot you will switch your brain off and switch on your autopilot, which we don’t want!↩︎