Chapter 12 ▶ Direct proof
Note: You should be familiar with the flowchart of proof in Chapter 10 before reading this chapter.
Welcome to our second method of proving conjectures: direct proof.
Direct proofs use algebra to move from \(P\) to \(Q\).
12.1 Steps
Make sure the conjecture is in the form If … then …. This is good practice for any method of proof, but especially direct proof.
What do you know? What information does \(P\) give you? What do you know about the subject of the conjecture?
How can what you know get you to the conclusion you need to make, \(Q\)?
Be aware!
You might have to try out different routes from \(P\) until you find one that gets you to \(Q\).
It is wrong to use \(Q\) in your proof. You of course should use it to guide your work, like a goal to reach, but \(Q\) isn’t a tool to be used in a direct proof. (See Assuming the thing to be proved is true in Chapter 9, section 4.)
12.2 Formal definition
Simply, prove that “If \(P\) then \(Q\).”
12.3 Conjectures
Exercise 12.1 Use the following examples to practise. Solutions are below.
Conjecture 12.1 : The sum of two even numbers is even.
Conjecture 12.2 : The square of an odd number is also odd.
Conjecture 12.3 : The sum of the first \(n\) positive integers is \(\frac{n}{2}(n+1)\).
Conjecture 12.4 : For any four consecutive integers, the difference between the product of the last two and the product of the first two of these numbers is equal to their sum.
Solutions:
Conjecture 12.1: First, we rewrite the conjecture,
Now we’re ready for a direct proof.
Proof. Since \(a\) and \(b\) are even, they can be written as \[\begin{align} a &= 2k \\ b &= 2l \end{align}\] where \(k\) and \(l\) are integers. Therefore the sum of \(a\) and \(b\) is \[\begin{align} a + b &= 2k + 2l\\ &= 2(k + l) \end{align}\] by factoring out 2.
As the sum of integers equals an integer, \(k + l\) must equal some integer. Let’s call it \(m\). Therefore we have \[\begin{align} a + b &= 2m \end{align}\] which is clearly even.Conjecture 12.2: First, we rewrite the conjecture,
Now we’re ready for a direct proof.
Conjecture 12.3: See https://www.youtube.com/watch?v=aaFrAFZATKU.
Conjecture 12.4: First, we rewrite the conjecture,
Now we’re ready for a direct proof.
Proof. Four consecutive integers can be write as \(a, a+1, a+2, a+3\).
Then the product of the first two will be
\[\begin{align} a(a+1) &= a^2 + a \tag{12.2} \end{align}\]
and the product of the last two will be
\[\begin{align} (a+2)(a+3) &= a^2 + 5a + 6 \tag{12.3} \end{align}\]
The difference between Equality (12.3) and Equality (12.2) is \[\begin{align} (a^2 + 5a + 6) - (a^2 + a) &= 4a + 6 \tag{12.4} \end{align}\]
We need to show this Equality (12.4) is the same as the sum of the four numbers, which is
\[\begin{align} a + a+1 + a+2 + a+3 &= 4a + 6 \end{align}\]
As this is the same as Equality (12.4), we are done.
Exercise 12.2 Some of these conjectures are false; disprove them by finding a counterexample. Some of them are true; prove them using a proof by exhaustion (from last class) or a direct proof (from this class).
Conjecture 12.5 : If \(a\) and \(b\) are both perfect squares, then \(ab\) is also a perfect square.
Conjecture 12.6 : The sum of two odd integers is even.
Conjecture 12.7 : All odd primes end with 1, 3, 7 or 9.
Conjecture 12.8 : If \(a\) and \(b\) are both odd, then the difference of their squares is even. (This means if you square two odd numbers and find the difference between these two squares, the difference will be even.)
Conjecture 12.9 : The sum of two consecutive integers is odd.
Conjecture 12.10 : The sum of three consecutive integers is odd.
Conjecture 12.11 : The sum of three consecutive integers is divisible by 3.
Conjecture 12.12 : The sum of three consecutive odd numbers is divisible by 3.
Conjecture 12.13 : The sum of two consecutive odd numbers is divisible by 4.
Conjecture 12.14 : For a right-angled triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides. This is the Pythagoras Theorem. Prove it algebraically with a direct proof using the picture below.
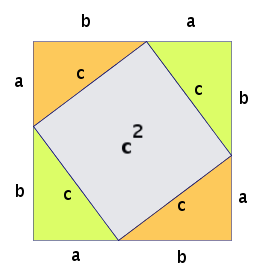
Conjecture 12.15 : The product of three consecutive integers is divisible by 6.
Conjecture 12.16 : There is no four-digit number that reverses its digits when multiplied by 4 (in other words, ABCD x 4 = DCBA).
Conjecture 12.17 : Summing two 3-digit numbers results in a 4-digit number.
Conjecture 12.18 : If a number is divisible by 4, then it is divisible by 2.
Conjecture 12.19 : If a number is divisible by 2, then it is divisible by 4.
Conjecture 12.20 : If \(a\) is a positive nonprime whole number and some prime number \(p\) divides \(a\), then some other prime \(q\) (\(q \neq p\)) also divides \(a\).
Conjecture 12.21 : If \(a + 4 > 0\), then \(a\) is positive.
Conjecture 12.22 : For any negative number \(a\), \(a^2 > a\).
Conjecture 12.23 : If \(a^2\) is divisible by \(2\), then so is \(a\).
Conjecture 12.24 : If \(a^2\) is divisible by \(3\), then so is \(a\).
Conjecture 12.25 : To multiply a two-digit number by \(11\), simply add the two digits of the number togetheIf the sum of the two digits is \(10, 11, 12, ..., 19\), carry the one over to the first number.r, then insert it in between the two digits.
For example \(11 \times 11 = 121\), \(23 \times 11 = 253\), \(77 \times 11 = 847\).
Conjecture 12.26 : In the picture below, the larger square is twice the area of the smaller square.
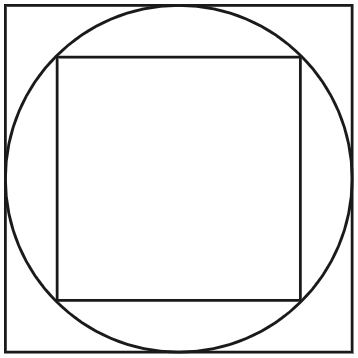
Figure 12.1: The figure shows a square inscribed in a circle, which is inscribed in another square.