Chapter 18 ▶ Proof by induction

One of the simplest, but most powerful methods of proof is induction. We use it to show that a conjecture is true for all integers above (and including) a specified integer.

18.1 The steps

There are two things to do:

Assume that the conjecture is true for \(a\), and show that the conjecture would also be correct for the next number \(a + 1\).
Show that the conjecture is true for the lowest value of \(a\), called \(a_0\). This is known the ‘base case.’

And you’re done!

18.1.1 The domino analogy

Think of this method of proof like a row of dominoes, and you want every domino to fall over:

Figure 18.1: A row of dominoes. Source: Pokipsy76 via commonswiki.

First, you make sure that each domino is spaced so that if the one before it falls, then it too will fall. This is proving that if the conjecture is true for \(a\), it’s also true for \(a+1\).

Next, you push the first domino. This is proving the conjecture is true for the base case, \(a_0\).

The result: all the dominoes will fall - https://www.youtube.com/watch?v=TE5RdFFgW0w.

18.1.2 When to use induction

We usually use a proof by induction when the conjecture:

is dealing with integers,
has an obvious base case, for example “for all positive integers” (base case = \(1\)), “for all three-digit primes” (base case = \(101\)), “for all odd numbers” (base case = \(1\)), etc.

18.1.3 Identifying the base case

It’s easy to identify the base case \(a = a_0\), as it will be obvious from the conjecture. For example, if the conjecture begins:

“For all integers greater than or equal to 2 …,” then your base case is \(a_0 = 2\).
“For all positive integers …,” your base case is \(a_0 = 1\).
“For all nonnegative integers …,” your base case is \(a_0 = 0\).
“For all integers greater than \(-10\) …,” your base case is \(a_0 = -9\).
“For all composite numbers …,” your base case is \(a_0 = 4\).⁵³

18.2 Formal definition

To prove \(P \Rightarrow Q\) for all \(a\) (where usually \(a \in \mathbb Z\)) by induction, show that

If \(P \Rightarrow Q\) for \(a\), then \(P \Rightarrow Q\) for \(a+1\)

and

\(P \Rightarrow Q\) for \(a_0\),

where \(a_0\) is the smallest example of \(a\).

18.3 Conjectures

Exercise 18.1 Use the following examples to practise proof by induction.

Conjecture 18.1 : For any positive integer \(a\), \(8^a - 1\) is divisible by \(7\).

Conjecture 18.2 : For any positive integer \(a\), \(2^a > a\).

Conjecture 18.3 : The sum of the first \(a\) positive integers is given by \(\frac{a(a+1)}{2}\).

Conjecture 18.4 : Every nonnegative integer is either even or odd.

Solutions:

Conjecture 18.1: This conjecture wants us to prove that all the numbers in the series \(7, 63, 511, ...\) are divisible by \(7\). It’s easy to see the first few are, but how to prove that all entries in this (infinite) list are?

As this conjecture deals with the positive integers \(1,2,3,...\), this is an obvious example of when a proof by induction could be useful (with base case \(a_0 = 1\)). Let’s try…

Proof.
Step 1: If \(8^{a}-1\) is divisible by \(7\), is \(8^{a+1}-1\)?

Well, \[\begin{align} 8^{a+1}-1 &= (8)8^{a} -1 \\ &= (7+1) 8^{a}-1 \\ &= (7) 8^{a} + 8^{a}-1 \end{align}\]

We know that \((7) 8^{a}\) is divisible by \(7\), and we’ve assumed that \(8^{a}-1\) is divisible by \(7\). The sum of two numbers divisible by \(7\) will also be divisible by \(7\).

Therefore, if \(8^{a}-1\) is divisible by \(7\), \(8^{a+1}-1\) is too.

Step 2: We should show that the conjecture is true for our base case, \(a=1\).

\[\begin{align} 8^1-1 &=8-1 \\ &=7 \end{align}\]

which is divisible by \(7\).

We are done.

Check that you’re happy with why exactly this proof is done:

The conjecture is true for \(a=1\).
We’ve shown that if the conjecture is true for \(a\), then it’s true for \(a+1\), so we know that the conjecture is true for \(a=2\) (without needing to check \(8^2-1\)).
And as the conjecture is true for \(a=2\), we know that the conjecture is true for \(a=3\) (without needing to check \(8^3-1\)).
And as the conjecture is true for \(a=3\), we know that the conjecture is true for \(a=4\) (without even needing to check \(8^4-1\)).
Etc. till infinity.

Conjecture 18.2:

Proof. https://www.youtube.com/watch?v=wNRvF6vx_go

A couple of things to note about this video:

He does Step 2 first, then Step 1. This is common. The order of the steps isn’t important.
He uses \(n\) instead of \(a\). It’s OK; it’s just a different letter.
He uses the mathematical symbol \(\forall\), which means “for all.” For example “AUCA student ID numbers are 4-digits long \(\forall\) students” or “\(a^2\) is even \(\forall\) even integers \(a\).”
At one point he introduces \(k\). Here, \(k\) is simply a specific value of \(n\).
At another point he writes \(22^k\) but he means \(2 \cdot 2^k\) or \(2 \times 2^k\). It’s clear from the context what he mean, however.

Conjecture 18.3:

Proof.
Step 1: Show that if the conjecture is true for \(a\), then it must be true for \(a+1\).

We assume that the sum of the first \(a\) positive integers is \(\frac{a(a+1)}{2}\). The sum of the first \(a+1\) positive integers would therefore be

\[\begin{align} \frac{(a+1)((a+1)+1)}{2} \end{align}\]

which was found by replacing any appearance of \(a\) with \(a+1\). Let’s simplify

\[\begin{align} \frac{(a+1)((a+1)+1)}{2} &= \frac{(a+1)(a+1+1)}{2} \\ &= \frac{(a+1)(a+2)}{2} \\ &= \frac{a^2+3a+2}{2}. \tag{18.1} \end{align}\]

But if the sum of the first \(a\) positive integers is \(\frac{a(a+1)}{2}\), then the sum of the first \(a+1\) positive integers is \((a+1)\) more than \(\frac{a(a+1)}{2}\), so

\[\begin{align} \frac{a(a+1)}{2} + (a+1). \tag{18.2} \end{align}\]

Let’s simplify Equation (18.2) and check whether this is same as Equation (18.1).

\[\begin{align} \frac{a(a+1)}{2} + (a+1) &= \frac{a(a+1)}{2} + \frac{2(a+1)}{2} \\ &= \frac{a(a+1) + 2(a+1)}{2} \\ &= \frac{a^2+a + 2a+2}{2} \\ &= \frac{a^2+3a+2}{2} \end{align}\]

which is the same as we found in Equation (18.1). We have proved that if the conjecture is true for the first \(a\) positive integers, it will be true for the first \(a+1\) positive integers.

Step 2: We should show that the conjecture is true for the base case. For this conjecture, the base case is \(a_0 = 1\), as we’re concerned with the first \(a\) positive integers and the first positive integer is 1.

The sum of the first 1 positive integers is 1. Let’s substitute \(a_0 = 1\) into \(\frac{a(a+1)}{2}\) and check we get this:

\[\begin{align} \frac{a(a+1)}{2} &= \frac{1(1+1)}{2} \\ &= \frac{2}{2} \\ &= 1 \end{align}\]

We’ve shown the conjecture is true for the base case, \(a=1\).

We are done.

Conjecture 18.4: For this conjecture, we’ll need a proof by induction using cases.

Proof.
Step 1: Show that if the conjecture is true for \(a\), then it must be true for \(a+1\).

Case 1: Consider two consecutive numbers \(x\) and \(y\). If \(x\) is even, it can be written as \(2k\), where \(k\) is some integer. As \(y\) is consecutive to \(x\), it must equal \(2k + 1\), which means it is odd. We have shown that odd numbers always follow even numbers.
Case 2: Consider two consecutive numbers \(x\) and \(y\). If \(x\) is odd, it can be written as \(2k +1\), where \(k\) is some integer. As \(y\) is consecutive to \(x\), it must equal \((2k + 1) + 1 = 2k + 2\) which can be written as \(2(k + 1)\), which means it is even. We have shown that even numbers always follow odd numbers.

Step 2: We should show that the conjecture is true for the base case. As the conjecture concerns nonnegative integers, our base case is \(a_0 = 0\). \(0\) is even, because \(0 = 2(0)\).

We are done.

Why are we done?? Because \(0\) is even, then \(1\) must be odd and because \(1\) is odd, \(2\) must be even, and so on, till infinity…

18.4 Going the “other” way

The method of proof by induction outlined above has two keys steps, proving the conjecture is true for the base case (the lowest possible value covered by the conjecture) and proving that if the conjecture is true for \(a\) it’s also true for \(a+1\). By these means, our proof applies up to (positive) infinity.

However, if you prove that the conjecture is true for the base case and show that if the conjecture is true for \(a\) it’s also true for \(a\) \(-\) \(1\), a proof by induction can apply all the way down to negative infinity. The only thing you change is step 2. Oh, and your base case might be something like \(a_0=-1\) or \(a_0=0\) for example.

For example, with Conjecture 18.4 above, instead of showing that odd numbers always follow even numbers and even numbers always follow odd numbers, you could show that even numbers always precede odd numbers (and that odd numbers always precede even numbers). Then, by using a base case of \(a_0 = -1\), you could prove this conjecture for all negative integers till negative infinity. (See conjectures 18.12 and 18.13 below.)

Exercise 18.2 Some of these conjectures are false; disprove them by finding a counterexample. Some of them are true; prove them using one (or a combination of more than one) of the methods we’ve met so far.

Conjecture 18.5 : \(8a - 1\) is divisible by \(7\) for any positive integer \(a\).

Conjecture 18.6 : For any positive integer \(a\), \(5^a - 1\) is divisible by \(4\).

Conjecture 18.7 : The sum of two consecutive positive integers is odd.
We have proved this theorem before, but try to prove it again using induction.

Conjecture 18.8 : The sum of the first \(a\) positive odd numbers equals \(a^2\).

Conjecture 18.9 : Any group of students is able to be split up into groups of twos, groups of threes, or a combination of groups of twos and threes.

Conjecture 18.10 : Any group of students greater than two is able to be split up into groups of threes, groups of fours, or a combination of groups of threes and fours.

Conjecture 18.11 : Any amount greater than or equal to 12 soms can be made using an infinite supply of 4-som and 5-som coins.

Conjecture 18.12 : Every negative integer is either even or odd.
Section 18.4 discusses using a proof by induction in the opposite direction (towards negative infinity). See Conjecture 18.4 for the nonnegative version of this.

Conjecture 18.13 : \(2^a > a\) for all negative integers \(a\).

Conjecture 18.14 : Every row of Pascal’s Triangle is a power of \(11\).
The first six rows of Pascal’s Triangle are shown below⁵⁴, but this conjecture says that every row (till infinity) is a power of \(11\). For example \(1\) is a power of \(11\) (\(11^0=1\)), \(11\) is a power of \(11\), \(121\) is a power of \(11\), \(1331\) is a power of \(11\), etc.

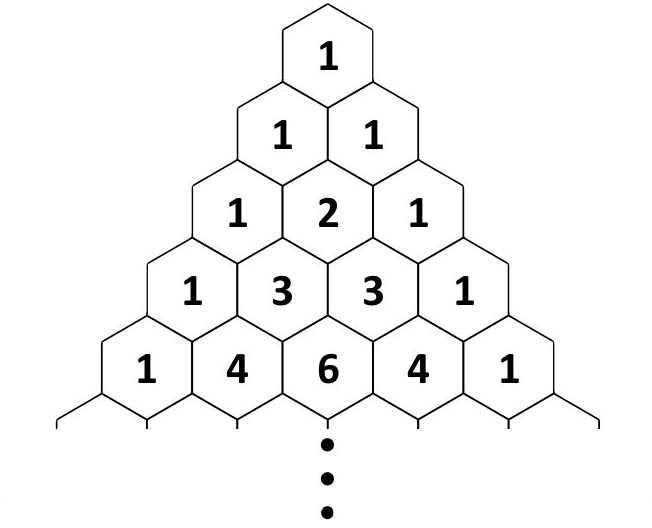
Conjecture 18.15 : \(1^2\), \(11^2\), \(111^2\), \(1111^2\), … are all palindromic numbers.⁵⁵

Conjecture 18.16 : The product of three odd numbers is odd.

Conjecture 18.17 : The product of any amount of odd numbers is odd.

Conjecture 18.18 : There are no two integers \(a\) and \(b\) where \(a^2 = b^3\), with \(a\), \(b > 1\).

Conjecture 18.19 : The interior angles of the octagon formed by joining the midpoint of each side of a square with each corner of the square are not all equal.
Hint: Draw the picture first!

Conjecture 18.20 : Squares of odd numbers are all one more than a multiple of \(8\).

Conjecture 18.21 : If \(a + b < 15\), then at least one of \(a\) and \(b\) is less than \(8\).

Conjecture 18.22 : There’s no positive integer \(a\) such that the deletion of its first digit divides it by \(2\).

Conjecture 18.23 : There’s only one positive integer that is equal to the sum of all the positive integers less than it.

Conjecture 18.24 : Every positive odd integer is equal to the difference of two perfect squares.

Conjecture 18.25 : If an integer \(a\) is not divisible by \(3\), then \(a^2 = 3k + 1\) for some integer \(k\).

Conjecture 18.26 : If \(a^2 = b^2\), then \(a = b\).

\(1\), whilst not prime, is not composite, as the definition of a composite number is a positive integer which has factor other than \(1\) and itself. In fact, \(1\) is the only positive integer that is neither prime nor composite.↩︎
Source: https://www.livescience.com/51238-properties-of-pascals-triangle.html.↩︎
A palindromic number is one that reads the same backwards as it does forwards, e.g. \(987789\) and \(434\). Similarly, a word is palindromic if it reads the same backwards as it does forwards, e.g. racecar and noon. Sentences can be palindromic too, usually by ignoring spaces and punctuation, e.g. “No lemon, no melon” or “Was it a cat I saw?”↩︎